Линейная регрессия: основы и применение

Линейная регрессия является одним из основных методов анализа данных и прогнозирования. Она используется для описания и предсказания зависимости между одной или несколькими независимыми переменными и зависимой переменной. В этой статье мы рассмотрим основы линейной регрессии и ее применение в различных областях.

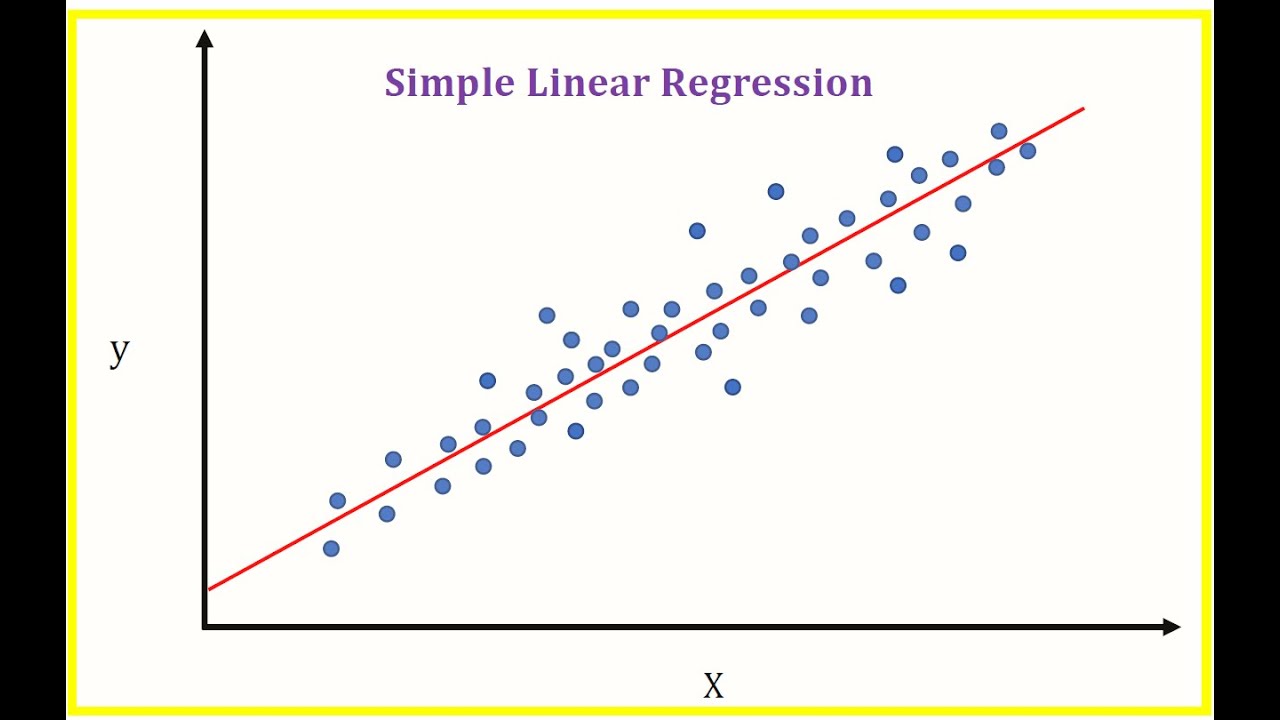
 Основы линейной регрессии

Линейная регрессия основана на предположении о линейной зависимости между независимыми и зависимой переменными. Модель линейной регрессии строится путем нахождения линейной функции, которая наилучшим образом приближает и объясняет данные. Формула линейной регрессии имеет вид:

y = b0 + b1*x1 + b2*x2 + … + bn*xn

где y — зависимая переменная, x1, x2, …, xn — независимые переменные, b0, b1, b2, …, bn — коэффициенты регрессии, которые определяют величину и направление влияния каждой независимой переменной на зависимую переменную.

 Применение линейной регрессии

Линейная регрессия широко применяется в различных областях, включая:

• Экономический анализ: линейная регрессия используется для анализа влияния экономических факторов на различные показатели, такие как объем продаж, цены на товары и услуги, безработица и другие.
• Маркетинг и реклама: модель линейной регрессии позволяет оценить эффективность маркетинговых и рекламных кампаний, определить влияние различных факторов на потребительское поведение и прогнозировать продажи.
• Медицина и здравоохранение: линейная регрессия применяется для анализа влияния факторов, таких как возраст, пол, образ жизни и генетические предрасположенности, на здоровье и развитие различных заболеваний.
• Физика и наука: линейная регрессия используется для моделирования и прогнозирования физических и научных явлений, а также для изучения зависимости между различными физическими величинами.
• Социальные и гуманитарные науки: линейная регрессия применяется для анализа социальных и гуманитарных данных, таких как образование, доходы, качество жизни и другие факторы, влияющие на социальное благополучие.

 Оценка и интерпретация результатов

Для оценки и интерпретации результатов линейной регрессии используются различные статистические показатели, такие как коэффициент детерминации (R-квадрат), коэффициенты регрессии, стандартные ошибки и другие. Они позволяют определить силу и статистическую значимость влияния независимых переменных на зависимую переменную.

 Ограничения и предпосылки

При использовании линейной регрессии необходимо учитывать ее ограничения и предпосылки, такие как линейность зависимости, независимость ошибок, отсутствие мультиколлинеарности и нормальность распределения ошибок. Нарушение этих предпосылок может привести к неправильным результатам и ненадежным выводам.

В заключение, линейная регрессия является мощным инструментом анализа данных и прогнозирования. Она находит широкое применение в различных областях и позволяет описывать и предсказывать зависимости между переменными. Правильная интерпретация результатов и учет предпосылок помогают получить надежные и информативные выводы из модели линейной регрессии.